自动机理论

正则语言

Concepts

DFA: 确定型有穷自动机
NFA: 非确定有穷自动机
正则语言：能被一个有穷自动机接受的语言就是正则语言
语言: 如果 A 是机器 M 所接受的所有字符串组成的集合,那么我们就说 A 是机器 M 的语言.也可以写作
L(M)=A 或者 M 识别 A.

DFA

Definition

有穷自动机是一个五元组 $(Q, \Sigma, \delta, q_0, F)$:
1. Q 是一个有穷集合,叫 状态集.
2. $\Sigma$ 是一个有穷集合,叫 字母表.
3. $\delta: Q \times \Sigma \rightarrow Q$ 是 转移函数.
4. $q_0 \in Q$ 是 起始状态.
5. $F \subseteq Q$ 是 接受状态.

example

下面是一个叫 M₁ 的有穷自动机

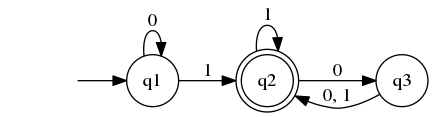
形式定义如下:

Q 是 {q₁, q₂, q₃}
$\Sigma$ 是 {0, 1}
转移函数 $\delta$ 由下表给出:

0 1

q₁ q₁ q₂

q₂ q₃ q₂

q₃ q₂ q₂

transformation rules
q₁ 是起始状态
F = |q₂|

	0	1
q₁	q₁	q₂
q₂	q₃	q₂
q₃	q₂	q₂

下面是一个M1的程序:

(define (m1 ss)
  (define tbl                     ;transformation rules
    '(((q1 . #\0) . q1) ((q1 . #\1) . q2)
      ((q2 . #\0) . q3) ((q2 . #\1) . q2)
      ((q3 . #\0) . q2) ((q3 . #\1) . q2)))
  (define accepted-states
    '(q2))

  (define m1-inner
    (let ([state 'q1])
      (lambda (input)
        (cond [(assoc `(,state . ,input) tbl) =>
               (lambda (entry)
                 (set! state (cdr entry))
                 (cdr entry))]
              [else (error 'Error "unkown state input pair ~a"
                           `(,state ,input))]))))

  (let* ([char-lst (string->list ss)]
         [ret (last (map m1-inner char-lst))])
    (if (memv ret accepted-states)
        'accept
        'reject)))

设M = $(Q, \Sigma, \delta, q_0, F)$ 是一台有穷自动机, $\omega=\omega_1
\omega_2 … \omega_n$ 是字母表 $\Sigma$ 上的字符串,如果存在 Q 中的状态序列:
r₀, r₁, …, r_n 满足下述条件:

r₀ = q₀
$\delta(r_i, \omega_{i+1})=r_{i+1}, i=0,1,2,…,n-1$
$r_n \in F$

则 M 接受 $\omega$.

正则运算

设 A 与 B 是两个语言, 定义正则运算并连接星号:
- union(并) : $A \cup B = {x| x \in A \ or \ x \in B }$
- concatenation(连接):
  $A \centerdot B = {xy| x \in A \ and \ y \in B }$
- star 星号:
  $A^* = {x_1 x_2 x_3 … x_k| k \geq 0 \ and \ \forall x_i \in A}$
property

正则语言类是所有正则语言组成的集合
1. 正则语言类在并运算下封闭 (closure under union)
2. 正则语言类在连接运算下封闭(closure under concatenation)

正则表达式

$(r)|(s)$ is a regular expression denoting the language $L(r) U L(s)$
(r)(S) is a regular expression denoting the language $L(r)L(s)$
$(r)$ is a regular expression denoting the language $L(r)^$
$(r)$ is a regular expression denoting the language $L(r)$

some extensions:

$(r)+$ is a regular expression denoting the language $L(r)+, r+ = rr*$.
$(r)?$ (zero or one)
$[abcd]$ is shorthand of $a|b|c|d$

NFA

DFA VS NFA
- DFA的每一个状态对于字母表中的每一个符号总是恰好有一个转移箭头射出,而NFA对
  于每一个状态对于字母表字母表的每一个符号可能有0,1
  或者多个箭头射出.
- NFA中箭头的标号可以是 $\varepsilon$, 而DFA不允许.
definition

非确定型有穷自动机是一个五元组 $(Q, \Sigma, \delta, q_0, F)$:
1. Q 是一个有穷集合,叫 状态集.
2. $\Sigma$ 是一个有穷集合,叫 字母表.
3. $\delta: Q \times \Sigma_\varepsilon \rightarrow \mathcal{P}(Q)$
  是 转移函数.
4. $q_0 \in Q$ 是 起始状态.
5. $F \subseteq Q$ 是 接受状态.
DFN的直观理解
1. 非确定性可以看做若干”过程”能同时运行的一类并行计算.当NFA分头跟踪若干选择
  时,这对应于一个过程分叉成若干个子过程,各子过程分别进行.如果这些子过程中
  至少有一个接受,那么整个计算接受
2. 把非确定性计算看作一颗可能性的树,树根对应计算的开始,树中的每一个分支点对
  应计算中机器有多种选择的点.如果计算分支中至少有一个结束在接受状态,则机器
  接受.
  
  该理解是这样操作的: 当读入字符串时,如果发现该字符串可以到达n个下一状态那么该节点就会有 n个子节点.如果发现有
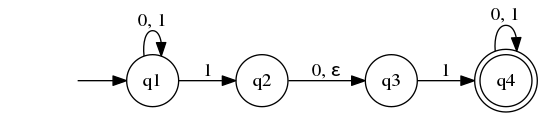
  $\varepsilon$ 箭头,那么就直接分裂出一个子节点.下图描述了 N1 对 010110的计算
property
1. 每一台 NFA 都有一台等价的 DFA与之对应
2. 正则语言类在并运算下封闭
  
  Proof: 假设有正则语言 A1 A2, 它们对应的 NFA为 N1 N2, 现在构造出一台NFA, 它能够识别出 A1 U
  A2, 构造的方法就是使用一个新的初始状态q₀, 而从 q₀ 上分别连一个
  $\varepsilon$ 箭头到N₁ 与 N₂ 的初始状态,见下图: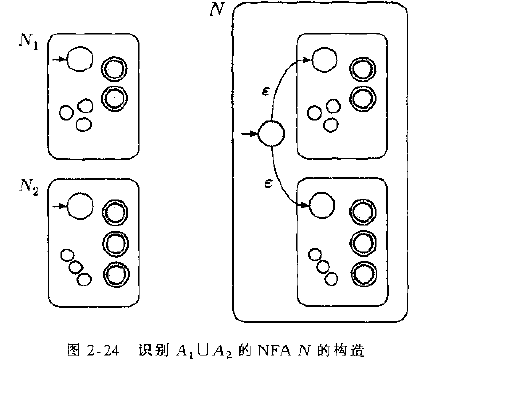
3. 正则语言在连接运算下封闭
  
  Proof: 假设有正则语言 A1 A2, 它们对应的 NFA为 N1 N2, 现在构造出一台NFA, 它能够识别出 A1
  A2, 构造的方法就是从N1的每一个接受状态都连一个 $\varepsilon$ 箭头到N₂
  的初始状态,见下图:
4. 正则语言类在星号运算下封闭